Let’s solve LeetCode problem 61: Rotate List.
The instructions are as follows:
Given the
headof a linked list, rotate the list to the right by \(k\) places.Constraints:
- The number of nodes in the list is in the range
[0, 500]-100 <= Node.val <= 1000 <= k <= 2 * 10^9
Let’s dive in!
Recalling array rotations
In a recent post, I solved this exact problem for arrays (LeetCode problem 189). The method was a triple-reversal procedure:
- Reverse the entire array.
- Reverse the first \(k\) elements.
- Reverse the remaining elements (after index \(k\)).
Let’s try an example. Suppose we have an array [1, 2, 3, 4, 5] and \(k = 2\). The solution is [4, 5, 1, 2, 3].
Applying each step gives us:
- Main reversal:
[5, 4, 3, 2, 1]. - Reverse first part:
[4, 5, 3, 2, 1]. - Reverse second part:
[4, 5, 1, 2, 3].
I see no reason why this wouldn’t work with a linked list too. Let’s implement it!
Defining the reverse function
Reversing a linked list is a bit more involved than reversing an array, as we have to carefully consider node pointers. Let’s assume we have two pointers:
head, which points to the first node in the part of list yet to be reversed.rHead, which points to the first node of the already reversed part of the list.
We want to make head point to the new first node of the reversed list and then solve the problem for the remainder of the non-reversed list.
I came up with an idea that involves another temporary pointer tmp.
We can add one new node to the reversed list as follows:
- Set
tmptohead. - Move forward in the non-reversed list via
head = head->next. - Set
tmp->nexttorHead. - Set
rHeadtotmp.
Let’s visualize one reversal step. As an example, let’s take a linked list with elements [1, 2, 3, 4, 5]. I used R, H, and T instead of rHead, head, and tmp for brevity.
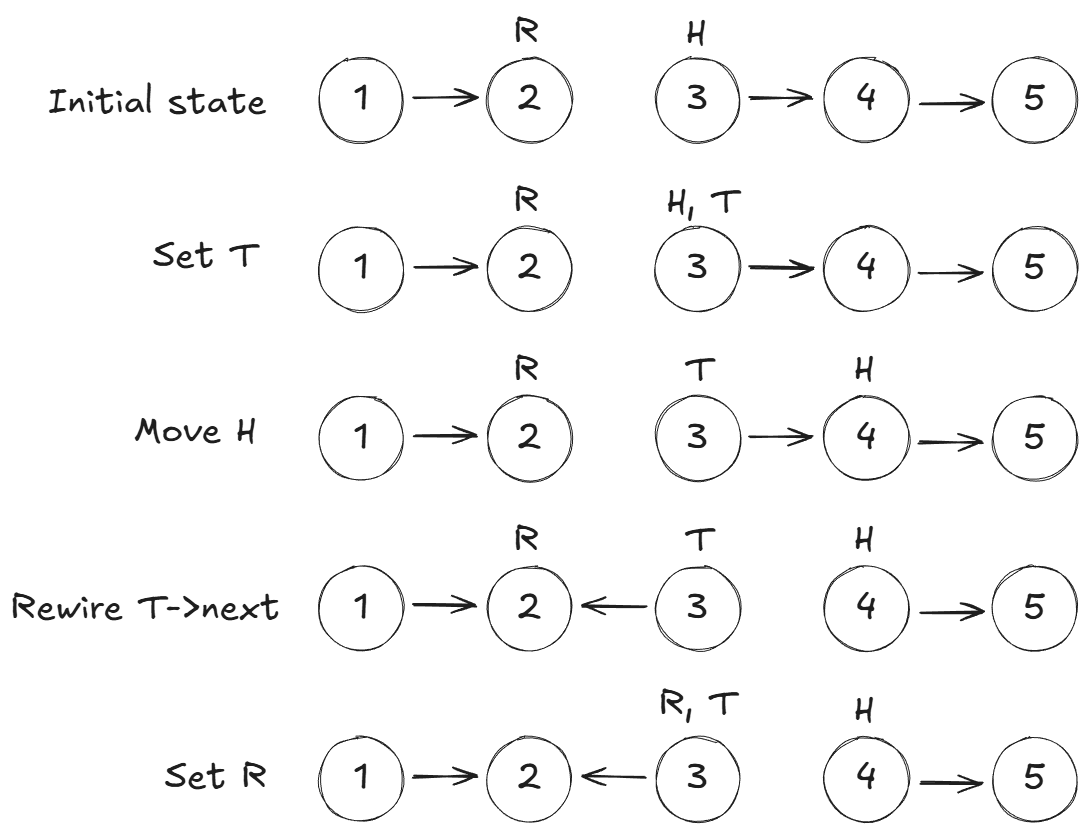
If we start with rHead = nullptr, then applying this for every node gives us the reversed list.
Let’s see the code.
ListNode* reverse(ListNode* head) {
ListNode* rHead = nullptr;
ListNode* tmp;
while (head) {
tmp = head;
head = head->next;
tmp->next = rHead;
rHead = tmp;
}
return rHead;
}
Say the linked list has length \(n\). The function only has to traverse the linked list once, which makes its time complexity \(O(n)\). The space complexity is just \(O(1)\) as we only need to hold two pointers.
Handling large values of \(k\)
Before applying the triple reversal procedure, let’s note that \(k\) may be greater than \(n\).
Since linked list rotations are cyclical, we can save lots of computation time by reducing \(k\) modulo \(n\) (i.e. \(k = k\mod n\)).
We could compute the length of the linked list in the reverse function, but since the number of nodes is at most 500, I just opted to compute it separately. The time lost is negligible.
The code below computes the linked list length and reduces \(k\). It only has to traverse the list once, making its time complexity \(O(n)\). Its space complexity is \(O(1)\), as it uses a single pointer and size_t object.
size_t length = 0;
ListNode* tmp = head;
while (tmp) {
tmp = tmp->next;
length++;
}
k %= length;
Applying the triple-reversal procedure
What’s left is to apply the reverse function.
Since we’re working with pointers, we have to take two extra steps compared to array rotations:
- Reverse the entire linked list, obtaining
rHead. - Sever the connection between the \(k\)-th and \(k + 1\)-th nodes. This prevents infinite loops when calling
reverse. Keep a pointersecondHeadto the node at index \(k+1\) to recreate the connection later. - Reverse the linked list starting at
rHead, obtaining an updatedhead. - Reverse the linked list starting at
secondHead, obtaining an updatedsecondHead. - Add the connection between the two lists:
rHead->next = secondHead.
Let’s see a diagram again. We can use [1, 2, 3, 4, 5] as the example with \(k = 2\). I used R, H, and S instead of rHead, head, and secondHead for brevity.
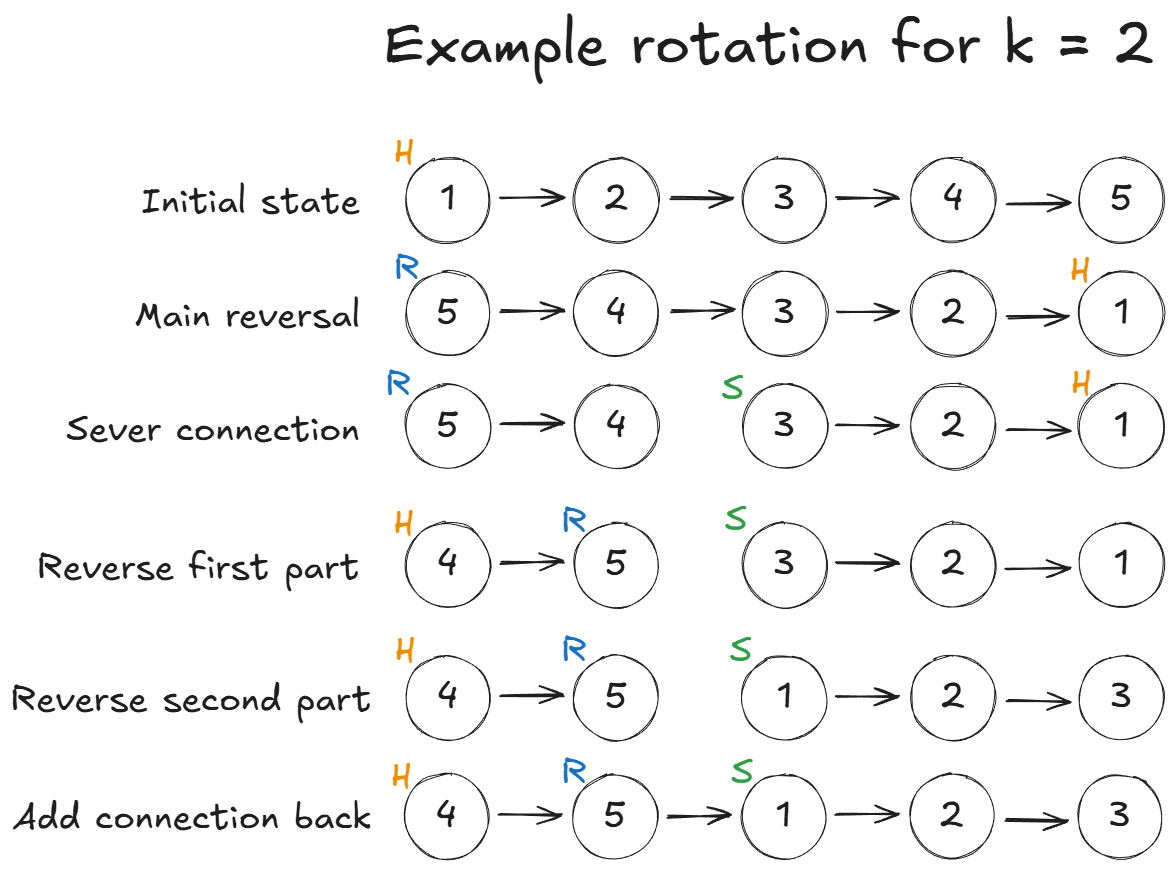
Two things happen in reverse first part step:
- We reverse the part of the list. While
rHeadpreviously pointed to the start of that list, it now points to the end. If the list was longer,rHeadwould still be at the very end. - We set
headto be the start of the list. This just means reusing an existing variable. Nothing happens to the second part of the list, except that we lose a reference to its end. However, we don’t need that reference anyway.
Each reversal takes \(O(n)\) time and \(O(1)\) space. Severing the connection and adding it back takes \(O(1)\) time and space. The entire rotation thus takes \(O(n)\) time and \(O(1)\) space.
Let’s see the full code.
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverse(ListNode* head) {
ListNode* rHead = nullptr;
ListNode* tmp;
while (head) {
tmp = head;
head = head->next;
tmp->next = rHead;
rHead = tmp;
}
return rHead;
}
ListNode* rotateRight(ListNode* head, int k) {
// Exit early
if (k == 0 || !head) {
return head;
}
// Reduce k
size_t length = 0;
ListNode* tmp = head;
while (tmp) {
tmp = tmp->next;
length++;
}
k %= length;
// Exit early
if (k == 0) {
return head;
}
// Main reversal
ListNode* rHead = reverse(head);
// Sever k-th connection
tmp = rHead;
while (k > 1) {
tmp = tmp->next;
k--;
}
ListNode* secondHead = tmp->next;
tmp->next = nullptr;
// Reverse first part
head = reverse(rHead);
// Reverse second part
secondHead = reverse(secondHead);
// Add connection back
rHead->next = secondHead;
return head;
}
};
The code runs in 0 ms (beating 100% of other solutions) and takes 16.32 MB memory (beating 63% – solutions with less memory usage apply some kind of LeetCode memory reduction tricks, so just for topping the leaderboards).
Thanks for reading! If you liked this post, you can support me on Ko-fi ☕. More LeetCode solutions coming soon :)